13.6 Summation Nodes
A summation node can be used to add together the values from portions of a tree. During calculations, the expected value (EV) of a summation node is equal to the sum of the EVs of all branches.
A chance node's EV is equal to the weighted average of its branches EVs. The summation node functions similarly except that the "weight" of each branch would be 100%.
The Legal tutorial example tree, LegalTree-Summation.trex, illustrates the use of the summation node.
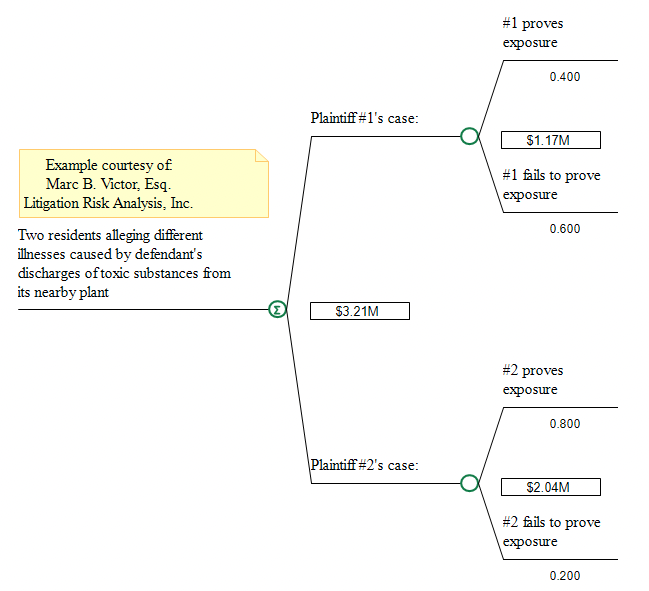
Note that the EV of the legal case will now reflect the sum of the EVs for the two individual plaintiffs as is shwon in the rolled back tree below.
A Summation Node can be used at the Root of a tree when you want to see multiple analyses on the same screen - for example, when you want to see the trees for multiple plaintiffs suing a defendant for similar reasons; or when a plaintiff has multiple claims involving different damages against a single defendant (think "construction defects").
However, this needs to be done with great caution, for two reasons:
-
Although it is true that the Expected Value of multiple suits or claims can be summed, it is not easy to sum their separate probability distributions (i.e., bar charts) - or even to answer the question "What's the chance of a $0 result overall?" So if it is important for your client to know - for example - the probability that the TOTAL award will exceed $X, then the suits/claims should be in a single tree that does not use a Summation Node.
-
Your probability assessments will typically be more realistic if you create just a single tree, because doing so will force you to think about questions like "If Plaintiff #1 fails to prove her medical causation - even though I think it is almost a sure thing she will prove it - do I really still think that Plaintiff #2 has as high as a 60% chance of proving his medical causation?"
The single tree LegalTree-NoSummation.trex illustrates this for the same problem first presented in Example Model > Legal > Summation for EV only. Note in particular the concept of "dependent/conditional" probabilities - the impact of the jury's Plaintiff #1 findings on the probabilities assessed for the jury's Plaintiff #2 findings. [To keep this example tree from growing too large, note that the damage awards have been treated as "perfectly correlated" - i.e., if the jury is "high" for one plaintiff it will be "high" for the other, and so on. But putting both plaintiffs in a single tree forces counsel to think about whether this is a reasonable assumption or not. If it isn't, the overall probability distribution will be different even though the overall expected value may not change.]
Note that some analyses are not supported for summation nodes - specifically probability distribution graphs. You can still run Roll Back, Rankings, Sensitivity Analysis and Probabilistic Sensitivity Analysis.
Also note that summation nodes cannot be placed to the right of a Markov node (in Healthcare models).
