22.9 Expected value of perfect information (EVPI)
Assume that you could buy information that perfectly predicted the outcome of a future uncertainty. What would this information be worth to you?
In a decision tree, the option to acquire perfect information (about a single uncertainty) can be modeled by moving the chance node representing the uncertainty to the left of a decision.
Although the uncertain event still follows the decision in time, the decision maker is assumed to have a perfect predictor of the event outcome before making the decision. Keep in mind that perfect information does not mean that you can control the event’s outcome, only that you can predict the outcome.
Ignoring for the moment the cost of the perfect information, the revised tree cannot have a worse expected value than the original tree, and may have a better expected value. This difference in expected value is referred to as the expected value of perfect information (EVPI).
While predictive information is rarely perfect, the usefulness of EVPI is in calculating a maximum reasonable price for information. If perfect information in a particular situation has a base value of x, one should certainly not pay more than x for imperfect information. To see how imperfect information is dealt with in decision analysis, see the section on Bayes Revision in Decision Trees .
How EVPI is calculated
Before trying TreeAge Pro’s shortcut for calculating EVPI in a decision tree, it is instructive to work through the extra steps required to calculate EVPI manually.
-
Open the Business tutorial example model, Stock Tree.trex.
-
Also open the Business tutorial example model, Perfect Information. This version of the investment problem shows the time reversal of the Market uncertainty and the decision.
The two trees are shown below.
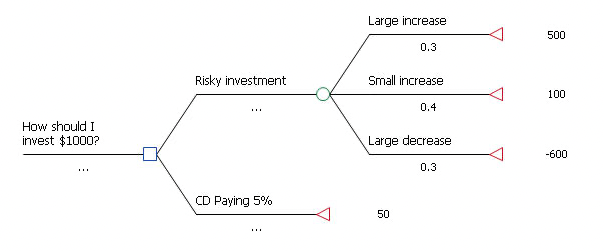
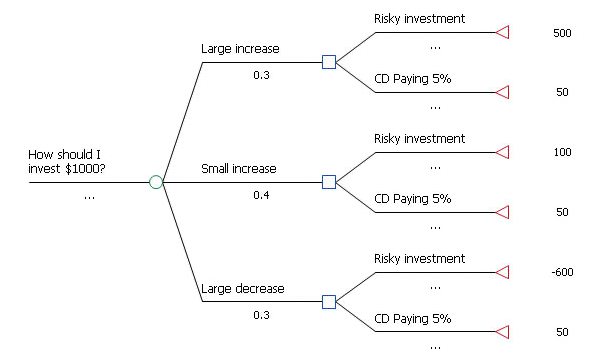
To calculate the EVPI manually:
-
Roll back Stock Tree. The tree’s expected value is $50 (equal to CD paying 5%’s value).
-
Roll back the Perfect Information tree. The root node’s expected value is $205.
-
To calculate EVPI, take the difference between the expected value of the Stock Tree and that of the Perfect Information tree. The difference is $155. (If you were minimizing costs rather than maximizing profit, you would subtract the perfect information value from the regular expected value.)
In the investment model, the expected value of having perfect information about the market activity is $155. This is the most you should be willing to pay to obtain this information, and it affords some basis for appraising to you the value of a less than perfect predictor of market activity.
Now, try TreeAge Pro’s shortcut for calculating EVPI in a tree. It requires only the original Stock Tree.
To calculate EVPI automatically:
-
Open the Stock Tree.
-
Select the Risky investment chance node and choose Analysis > Expected Value of Perfect Info.
A dialog reports the value of $155.

It is also possible to calculate EVPI automatically in a decision tree when the same event appears in more than one strategy, as in example shown below. The assumption in the model is that each of the two stock investments under consideration is followed by the same uncertainty — whether the market will be up or down at the end of the year.
In order to calculate EVPI in this model, both market uncertainty chance nodes must be selected.
To calculate EVPI for the same chance node in multiple paths:
-
Before choosing Analysis > Expected Value of Information, select all nodes in the tree which represent the same event.
If multiple chance nodes are analyzed, they:
-
must be descendants of the same decision node;
-
must be “siblings”; and
-
must have identical branches using identical probabilities. It does not matter if there are differences in the subtrees further to the right.
If there is more than one decision prior to the selected chance event, TreeAge Pro will prompt you to identify the decision for which EVPI should be calculated.
Avoiding EVPI errors
It is important to understand that it is possible to force invalid EVPI calculations. For example,
-
Open the Oil Drilling Problem tree again.
-
Select the Drill for Oil node in the No Soundings subtree and choose Analysis > Expected Value of Perfect Info.
In the resulting dialog boxes, you are presented with the option of having the analysis performed at the root, soundings decision node or at the drilling decision.
Performing the calculation at the No Soundings node is similar to the analysis undertaken above in connection with the EVPI tree. It certainly makes sense to calculate the value of knowing the state of oil reserves before deciding whether or not to drill.
However, what if you perform the EVPI calculation at the root decision node? The value reported is $437,632, significantly higher than at the No Soundings node. Is this a meaningful EVPI calculation?
The structure of the tree already includes the option of securing imperfect information in the form of a seismic test — this is the initial decision. Performing EVPI by placing the chance node representing the uncertain amount of oil to the left of this decision is meaningless. Having already received perfect information, the decision as to whether to obtain additional imperfect information regarding the same subject should have no value or relevance. Refer to the Bayes Revision in Decision Trees section for more information on imperfect information.
