Nesting or linking Markov models

35.5 Nesting or linking Markov models

TreeAge Pro includes powerful functions – for example, Node(), Global(), GlobalN(), and User() — that can perform tasks such as:

nest one Markov model within another
link multiple terminal nodes to one Markov model
combine a Markov microsimulation with expected value analyses

Function syntax is described in more detail in the Variables: Named Model Values section and the Tools and Functions for Complex Trees section. These functions are complex, and we recommend other more typical model building structure above using this approach.

The Special Features tutorial example tree "Node Function" illustrates how to refer to one part of a model from another. The Tree function is similar except it refers to a separate model.

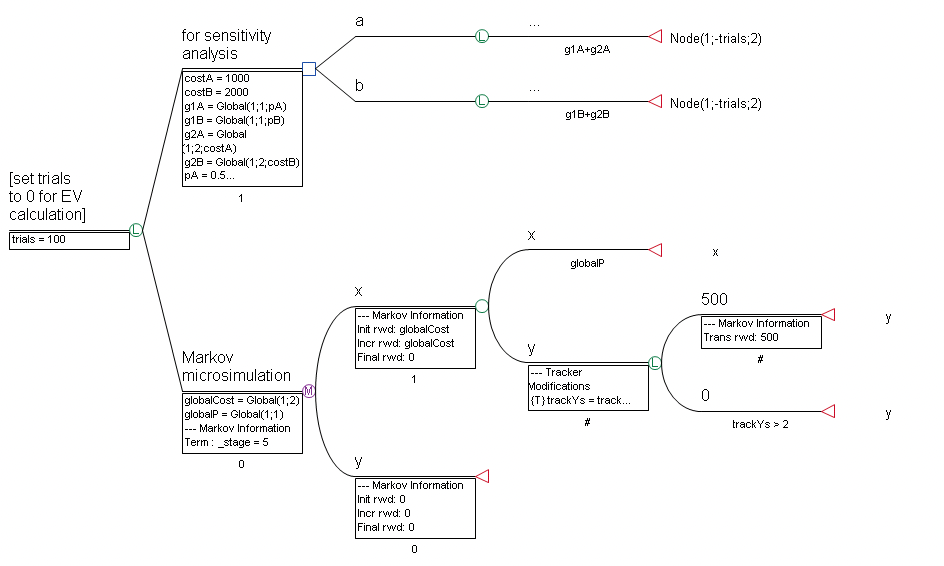
The top arm is set up for an expected value calculation and its decision node includes two strategies both linked via the Node() function to the same Markov model at the bottom. Each strategy passes distinct values to the Markov process using the Global() function. The Node() function then calculates the Markov model using microsimulation trials (even during non-simulation analyses of the top decision node).

The Node() function’s arguments are used to select a node in the tree and to determine what kind of calculation to use at that node. The syntax is:

Node(attribute; method; branch; …)

In CE models, the attribute argument determines whether to return cost or effectiveness (-1 calculates and returns cost; -2 returns effect from previous calculation; -11 returns cost from previous calculation; -12 calculates and returns effect). In non-CE models, as in the example, use any number other than 0 (which returns 0).

For the method argument, use 0 to calculate the expected value; or specify a negative number to average that number of microsimulation trials (e.g., -100 to run 100 trials), as in the example.

The third and subsequent branch arguments are branch numbers used to select a node starting with a branch of the root node.

In the tree, the complete expression Node(1;-trials;2) returns the cumulative reward (attribute 1), based on the average of 100 trials (method -100) at the Markov microsimulation node (branch 2).

The Global() function is illustrated in this example as well. However, it is not a required element of linking Markov trees. Global matrices can be used to store transient values when it is helpful, such as when you want to report the changing values of simulation tracker variables used in a subsidiary Markov process.

The following syntax is used to calculate and store a value in a cell in the Global matrix:

Global(row; column; expression)

The function returns the value of the calculated expression, as well as stores it in the Global matrix. The first cell in the global matrix is at row=1, column=1. Up to ten thousand cells are currently supported.

The following syntax can be used to reference a value saved to the global matrix:

Global(row; column)

The contents of the global matrix can be dynamically saved to a text file (or emptied) using the third syntax of the Global() function:

Global(value)

If the value evaluates to a non-zero number, the contents of the global matrix are silently saved to a text file in the tree’s directory. A zero value will empty the matrix. Refer to the Tools and Functions for Complex Trees section for more information.

In the example model, the variable definitions for g1A, g1B, g2A and g2B store information in the Global matrix. The definition g1A = Global(1;1;pA) stores the value pA in row 1, column 1 of the Global matrix.

At the unnamed branch of node a, the g1a and g2a are executed to generate a non-zero probability for the logic node, thereby placing the "a-related" values in the Global matrix. For the b strategy, the "b-related" values are placed in the Global matrix.

When the Markov model is evaluated (via Microsimulation) for each strategy by the Node function, the appropriate values are used when referenced in the Global matrix.

Additional notes on the Node() function:

Node() function syntax is described in more detail in the Tools and Functions for Complex Trees section. The related Tree() and Global() functions are also covered in detail there.
Trackers are not reset to 0 at the beginning of trials run by the Node() function. This is intentional in order to allow communication between the calling and called nodes.
Trials run by the Node() function do not resample distributions automatically (even if their properties are set to sample per trial). To force a sample, use the Dist(N; 1) syntax or DistForce(N). To control the sampling rate, put the force sample expression in a tracker evaluation (outside a Markov process, for example).
The second parameter of the Node() function, possibly specifying a number of simulation trials to be run, can be given a number after a decimal place to indicate that a statistical measure other than the mean should be used from the set of trials. Again, refer to the Tools and Functions for Complex Trees section.