15.1 Entering Upstream Payoffs Along Patient Pathways

In Decision Trees, every pathway from the root node to a terminal node within the model represents a scenario. By default, you assign value(s) for each scenario by entering payoffs at the terminal node. This accounts for all values accumulated along the patient pathway (review this for Decision Trees in the section Entering probabilities and payoffs).

This section describes an alternative way to assign value(s) by entering upstream payoffs at any node along the pathways. This allows you to enter the values at the points in the pathways where that value is naturally accumulated.

We will use the Healthcare Example Model HC-Tree-UpstreamPayoffs.trex to illustrate this technique. This model already contains the appropriate Tree Preferences settings and Upstream Payoff entries, but below we will review how these would be set up.

Setting Up the Model to add Upstream Payoff Entry

Turn on the upstream payoff entry option via Tree Preferences:

• Open Tree Preferences.

• Navigate to Calculation > Payoffs.

• Check the box to “Allow payoffs prior to terminal nodes”.

Upstream payoffs are shown below each node. You can choose to also show terminal node payoffs below those nodes via Tree Preferences (not done in example model).

• Open Tree Preferences.

• Navigate to Display > Payoffs.

• Check the box to “Show active payoffs below terminal nodes”.

Entering Upstream Payoffs

The HC-Tree-UpstreamPayoffs.trex model utilizes this option to accumulate treatment costs at the nodes in the model where they occur. Note that even the terminal node payoffs are shown under the node due to the payoff display Tree Preferences setting.

In this model, there are 6 nodes where costs are accumulated.

• Standard Treatment: Radiation. The cost of radiation occurs here (cRadiation).

• New Treatment: Surgery and Radiation. The costs of radiation and surgery occur here (cRadiation + cSurgery).

• Radiation eradicates tumor (twice): The cost of followup treatment occurs here in both treatments (cFollowupAnnual*effEradicated).

• Radiation fails to eradicate tumor (twice): The cost of followup treatment occurs here in both treatments (cFollowupAnnual*effNotEradicated).

With the default payoff settings, all values would have been accumulated in a payoff formula at each terminal node, as you can see in the figure in the section Entering probabilities and payoffs. For example, at the Radiation eradicates tumor node in the first strategy, the formula would have also included values accumulated at the upstream node Standard Treatment: Radiation (cRadiation + cFollowupAnnual*effEradicated).

To enter upstream payoffs:

• Select the node at which the value should be accumulated.

• Open the Payoffs View (from the Views menu).

• Enter the value accumulated at that node.

The figure below shows the Payoff View, editing the payoff for Standard treatment: Radiation.

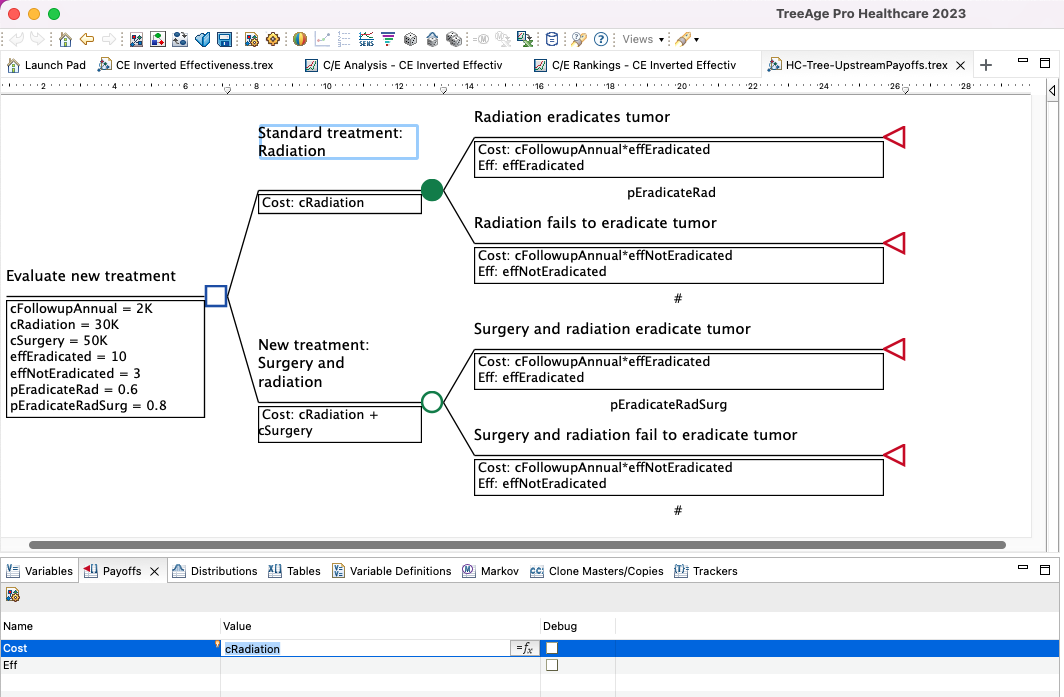
Once entered, you will then see the payoff shown below the node where it was entered.

You can also enter payoffs by Right-Clicking on any node and choosing Edit Payoffs from the context menu.

The payoff entry at an upstream node is then automatically applied to any scenario that passes through this node. If the model used the traditional payoff entry technique, this is the equivalent to adding that value to a payoff formula at each terminal node to the right of that node.

Analysis with Upstream Payoffs

When you analyze the decision tree, the model will accumulate the payoffs for every node along the scenario pathway from the strategy node to the terminal node.

Roll the model back and see the calculation of each scenario using payoffs entered across all nodes in the scenario.

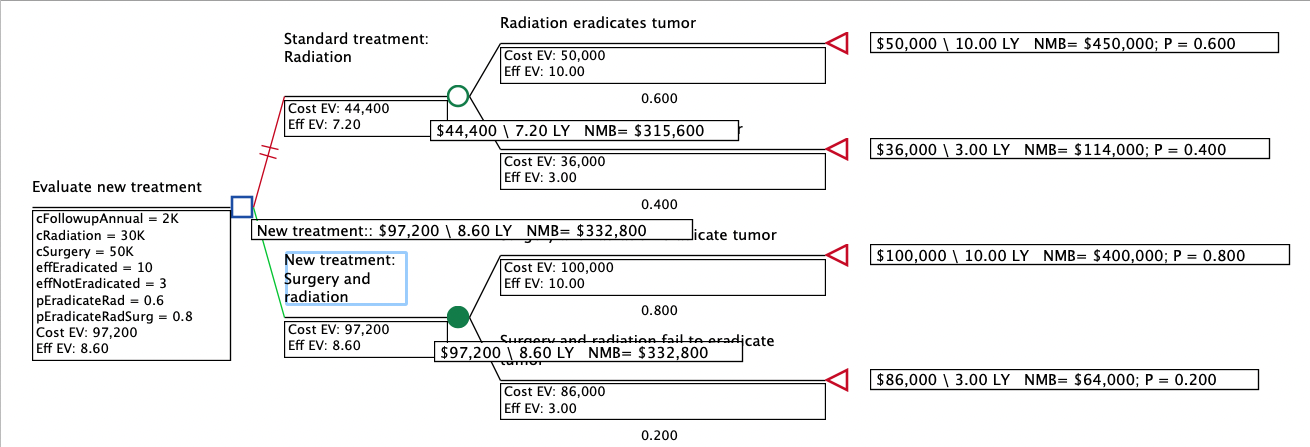
Note the final cost values of the scenarios that end at the terminal nodes below.

• Radiation eradicates tumor: $30K + $20K = $50K

• Radiation fails to eradicate tumor: $30K + $6K = $36K

• Radiation and Surgery eradicates tumor: $30K + $50K + $20K = $100K

• Radiation and Surgery fails to eradicate tumor: $30K + $50K + $6K = $86K