13.7 MultiNormal Distributions and Correlated Inputs
Model inputs can be correlated such that changes in one input are related to changes in other input(s). If you sample these inputs from independent distributions, this correlation is ignored. If correlations are ignored within the context of probabilistic sensitivity analysis, it can lead to more variance in your results than is realistic.
Input correlation can range from -1 to 1.
-
1 represents 100% correlation between inputs
-
0 represents no correlation between inputs
-
-1 represents 100% correlation in the opposite direction between inputs
To incorporate correlations when sampling values, you can use a MultiNormal distribution. MultiNormal distributions include multiple correlated variates and generate correlated samples for each of those variates. For example, if you have three correlated inputs, you would create a single MultiNormal distribution with three correlated variates, generating three sets of correlated samples.
The rest of this section describes how to create and use MultiNormal distributions for parameters in the context of Probabilistic Sensitivity Analysis (PSA). But you could also use MultiNormal distributions for patient characteristics in the context of Patient Simulation (Microsimulation).
Correlation Example Model
The Healthcare tutorial example model MultiNormal Distribution Correlation.trex is a Cost-Effectiveness decision tree comparing two treatments.
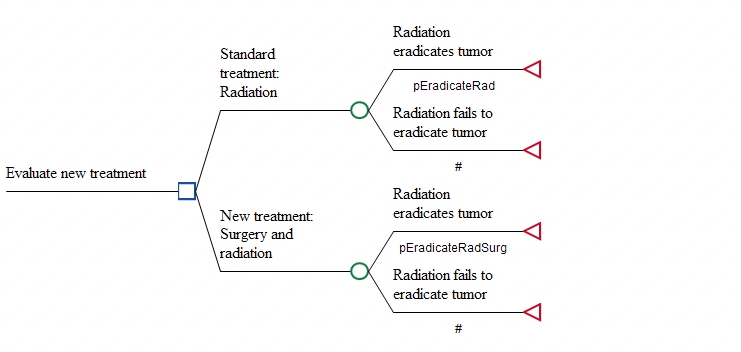
In each strategy, the patient pathways depend on the probability of eradicating the tumor. The probabilities in the two strategies are different – as represented by the variables pEradicateRad and pEradicateRadSurg.
For Probabilistic Sensitivity Analysis (PSA), those variables reference distributions. The model is set up to sample probabilities either with or without correlation between the two probability inputs. That way we can examine the impact of correlation on the PSA results.
-
No correlation – set variable correlatedSw = 0. The two probabilities are sampled from independent normal distributions.
-
Correlation – set variable correlatedSw = 1. The two probabilities are sampled from a single MultiNormal distribution which generates two correlated samples.
We will examine the results from PSA with and without correlation later in this section. Note: typically beta distributions would be used for probability parameters, but normal distributions are used in this example.
Creating a MultiNormal Distribution
Although the example model TreeAge MultiNormal Distribution Correlation.trex used in this chapter already has the MultiNormal distribution created, this section describes how to create one.
-
Open the Distributions View.
-
Click the “+” button to create a new distribution.
-
Enter the name of the distribution.
-
Scroll down the list of distribution types to select MultiNormal.
-
Click the Edit Matrix & Options button (See figure Screenshot #1). A second dialog “Edit Matrix & Options” will open (See figure Screenshot #2)
-
Enter the number of variates (minimum 2).
-
Select the appropriate Matrix type based on the form of your correlation data. This likely depends on the software used to generate the correlations.
-
Click on the column headings above the matrix and enter names for each variate within the MultiNormal distribution (optional) (See figure Screenshot #2 where Radiation and Rad_Surg have been entered as the column headings).
-
Enter the correlation data into the matrix grid.
-
Enter mean values for the individual variates.
-
Enter standard deviation (or scaling) values for the individual variates. Note that matrix types have variance built-in, so you would not enter the variate standard deviations.
-
If you have the matrix, mean and standard deviation data in Excel, you can copy and paste the data directly into the Matrix dialogue. Use the copy and paste buttons above the matrix.
-
Click OK to return to the Add/Change Distribution dialog.
-
In this example, the resampling rate is “Resample per EV” for use in PSA, which is what we want in this context.
-
Click OK to save the distribution.
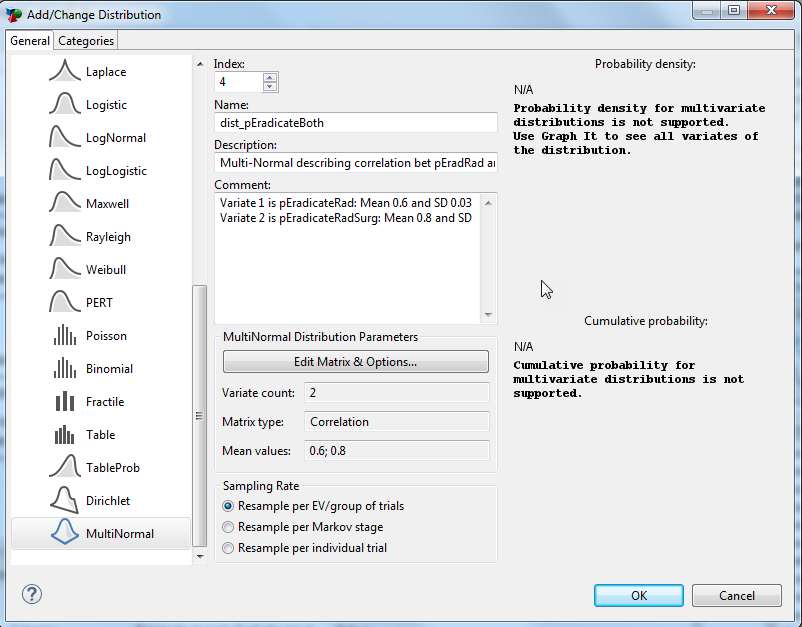
Screen shot #1
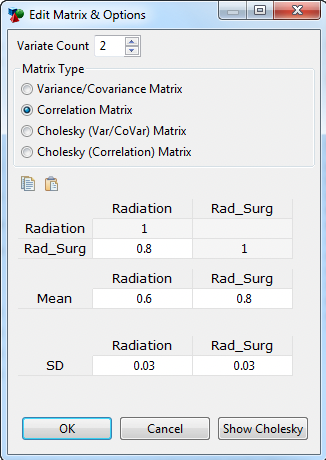
Screenshot #2
For the top two matrix types shown in Screenshot #2 above – Variance/Covariance and Correlation – TreeAge performs the Cholesky decomposition prior to sampling. Use the "Show Cholesky" button to show the calculated Cholesky Matrix as per TreeAge.
For the second two matrix types – Cholesky (Var/Covar) and Cholesky (Correlation) – the Cholesky decomposition has already been incorporated into the matrix, so TreeAge Pro does not apply it again. Depending on the software you have used to generate the correlations, you can enter data in any of these 4 formats.
Once your MultiNormal distribution is created, select the distribution in the Distributions View and click the "Graph It" icon within the Distributions View toolbar to see the samples generated for each variate of the MultiNormal distribution.
Referencing the MultiNormal Distribution in the Model
Although the Healthcare tutorial example model MultiNormal Distribution Correlation.trex used in this chapter already has the MultiNormal distribution incorporated, this section describes how it is referenced.
As with any distribution, it must be referenced within the model to have any impact on results. Many distributions just return a single value each time they are sampled, and these would be referenced directly, that is pVariable = dist_for_pVariable. Distributions such as MultiNormal and Dirichlet that have variates (that is they can return several values) must be referenced differently, so you can specify the variate you want. The two forms are presented below.
-
By name: Dist(“DistName”; "VariateName")
-
By index: Dist(DistIndex; VariateIndex)
You can also reference the distribution by name, and the variate by index or vice versa. Note that name entries are always placed in quotes, while index entries are not.
In our example model, the MultiNormal distribution is referenced with the first form above, but it is used only when correlationSw = 1. Therefore we see the following definitions:
-
pEradicateRad = if( correlatedSw=1 ; Dist("dist_pEradicateBoth"; "Radiation"); dist_pEradicateRad)
-
pEradicateRadSurg = if( correlatedSw=1 ; Dist("dist_pEradicateBoth"; "Rad_Surg"); dist_pEradicateRadSurg)
When running PSA with the variable correlationSw = 0, samples for the probabilities are assigned from two independent Normal distributions – dist_pEradicateRad and dist_pEradicateRadSurg. When running PSA with correlationSw = 1, samples for the probabilities are assigned from two variates of the MultiNormal distribution.
Impact of Correlation on PSA Results
To see the impact of parameter correlation, we can run PSA on the model first without correlation (correlationSw = 0), then with correlation (correlationSw = 1). In this model there is a high correlation between the parameters (0.8), so we expect the probabilities to change in a similar manner from sample to sample.
We specifically look at the ICE Scatter plot to illustrate the impact of parameter uncertainty – first without correlation, then with correlation.
PSA results - ICE Scatterplot with no correlation (correlationSw = 0)
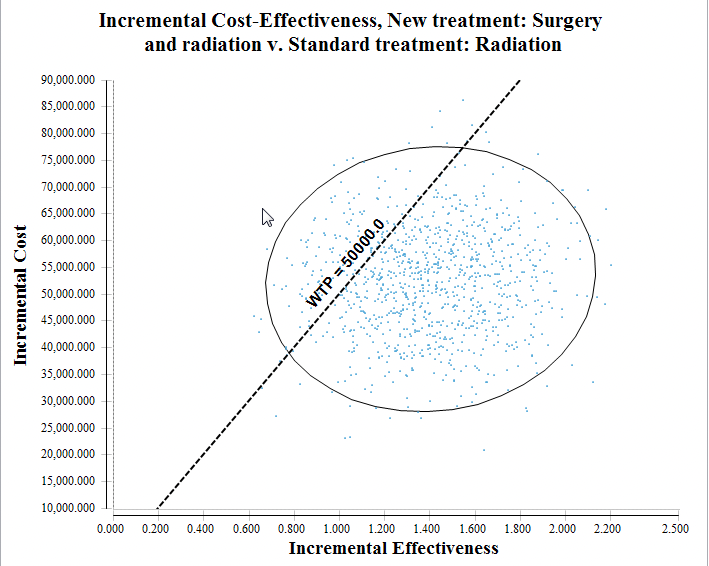
Without correlation, incremental effectiveness variance ranges from around 0.6 to 2.3.
PSA results - ICE Scatterplot with correlation (correlationSw = 1)
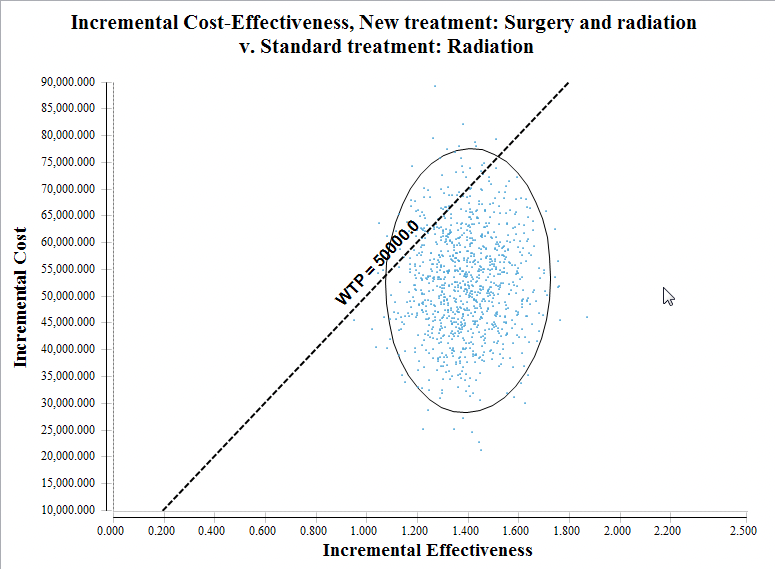
In the figures above, with correlation, incremental effectiveness variance ranges from around 0.9 to 1.8.
With high correlation between the sampled probabilities, the effectiveness values for the two strategies change together. This reduces the incremental effectiveness between the strategies' results. The reduction in the incremental cost range is less visible because incremental cost is also affected by a separate distribution dist_cSurgery.
