20.5 The Tree( ) Function

TreeAge Pro includes a variety of special functions which can be useful in complex models. These functions are described in the next several sections and include Node(), Tree(), User(), and Global().

The Tree() function allows you to return a calculated value from another tree. For example, you could have two separate Markov models defined for specific strategies for treating a disease. You could then have a third tree with a decision node that uses the Tree() function to refer to each strategy tree.

The Tree() function is one of a number of TreeAge functions available which take double-quoted string arguments rather than just arguments that can be evaluated numerically. Like all functions, however, the Tree() function returns a numeric value.

For the purposes of this documentation, the tree relationship is described as a calling tree, using the Tree function to access a target tree.

It is recommended that Tree() functions be carefully tested in simple models before being used in complex models.

The Tree() function syntax is described in the table below:

Function Syntax	Description
Tree( "target tree"; "calculation" )	Opens a hidden copy of the specified tree or package file, and returns the results of the specified calculation. The target tree remains open for additional Tree() function calls. The "target tree" argument specifies the path and filename of the target tree to open for calculation. However, if the file is in the same directory as the calling tree, only the filename is needed. The "calculation" argument defines the calculation to be performed on the target tree. Usually the Node() function will be used here, in order to calculate a specific node in the target tree. Example usage: utilXYZ = Tree( "c:\my docs\projects\xyz.tre"; "Node(1;0)") The Node() function, in this case, performs a simple expected value calculation at the root node of the target tree.
Tree( "target tree"; "calc"; 1 )	Same as above, but if the target tree is already open and visible, the linkage is left intact after the calculation; this allows analysis commands like rollback to be used on the visible target tree for debugging purposes. Note that if you use this option, the variables passed to the target tree will remain in place for further calls to that tree. If you are calling the target tree with other variable definitions later in the model, do not use the third argument.
Tree( "calculation" )	Can be used during an ongoing Tree() function evaluation in order to perform the given calculation at the root node of the current target tree.
Tree( integer 0 )	Closes any open, hidden target trees. Use this, for example, if you open a target tree using the File menu and save changes to it. This will cause the next Tree() function call to reload the target tree file from disk.

When the function opens/accesses a target tree, normally a temporary linkage is created; the target tree’s root node becomes the "child" of the calling node. The power of the Tree() function is that a target tree can use variable definitions from the calling tree or to the left of the calling node. This works very much like variables in cloned subtrees. The trick is that the variable can be referenced in the target tree while having no definitions; the definitions can instead be in the calling tree. Note that the variable name must be declared in the target tree’s Variables list, although it would not be defined in the target tree. The target tree must be opened before the roll back to create this active connection.

The function's primary use is for modularization of complex trees. For example, it might offer an alternative to memory-intensive models in which hundreds or thousands of cloned copies of a Markov model are created. For example, 1000 terminal node payoffs could use the Tree() function to calculate the same Markov model, just with different variable definitions (rather than attaching 1000 clones of the Markov subtree). Calculation speed in most models will be better if the Tree() function is not used, and clones are used instead; expressions in the hidden tree that reference a variable defined in the calling tree cannot be optimized. However, using clones (or regular copies) can sometimes result in a tree whose memory requirements exceed available physical memory, resulting in an extreme decline in calculation speed. Building smaller trees linked by the Tree() function would be a good solution in this case.

The following example uses three Special Feature tutorial examples: Tree Function Syntax.trex, Node Function Syntax.trex and Node Function Variable.trex.

• Tree Function Syntax: Calling tree that uses the Tree function to call the other two trees.

• Node Function Syntax: Self-contained tree referenced at the Lottery node.

• Node Function Variable: Same as above except that it needs to receive a definition for the variable GetDefFromParent from the Tree Function Syntax tree.

Let's look at the Tree Function Syntax tree - both its syntax (top) and the roll back results (bottom).

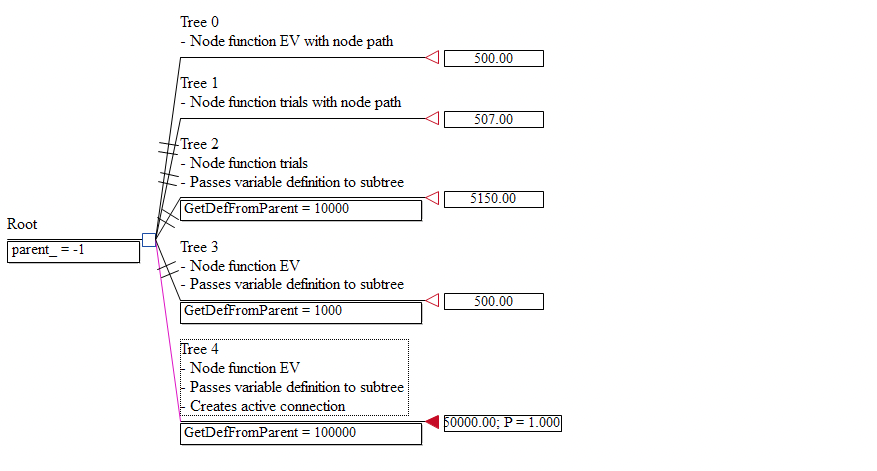
The Tree 0 terminal node calls for the expected value of the Node Function Syntax tree at the Lottery node, yielding a value of 500.

The Tree 1 terminal node runs 100 trials on the Node Function Syntax tree at the Lottery node, yielding a value near, but not equal to 500.

The Tree 2 terminal node runs 100 trials on the Node Function Variable tree at the Lottery node. The variable definition for GetDefFromParent (10,000) is passed from that node to the Node Function Variable tree. This yields a value near, but not necessarily equal to 5,000.

The Tree 3 terminal node calls for the expected value of the Node Function Variable tree at the Lottery node. The variable definition for GetDefFromParent (1,000) is passed from that node to the Node Function Variable tree. This yields a value of 500.

The Tree 4 terminal node calls for the expected value of the Node Function Variable tree at the Lottery node. The variable definition for GetDefFromParent (100,000) is passed from that node to the Node Function Variable tree. This yields a value of 50,000. Because the Tree function contains a third argument (1), the connection from the tree to the target tree is maintained, allowing you to roll back the Node Function Variable Tree with the GetDefFromParent variable definition intact.

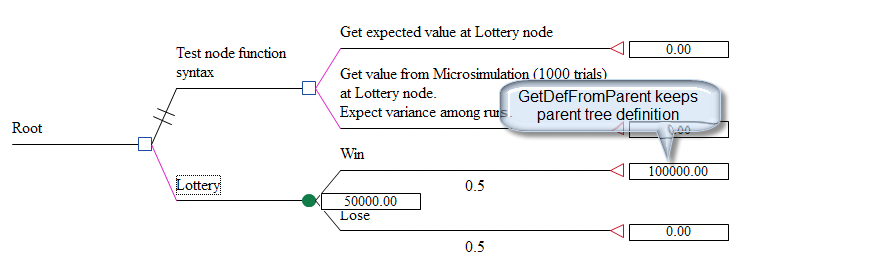
In the figure above, the payoff expression at the Win node is GetDefFromParent. This evaluates to 100,000 based on the intact variable definition from the Tree Function Syntax tree.

A simpler and perhaps more realistic example is found in the Legal tutorial example models Legal-MainTree.trex and Legal-Subtree.trex. In this example, the subtree is used to determine the probability of proving negligence. The main tree then pulls that probability into the larger legal model considering damages.

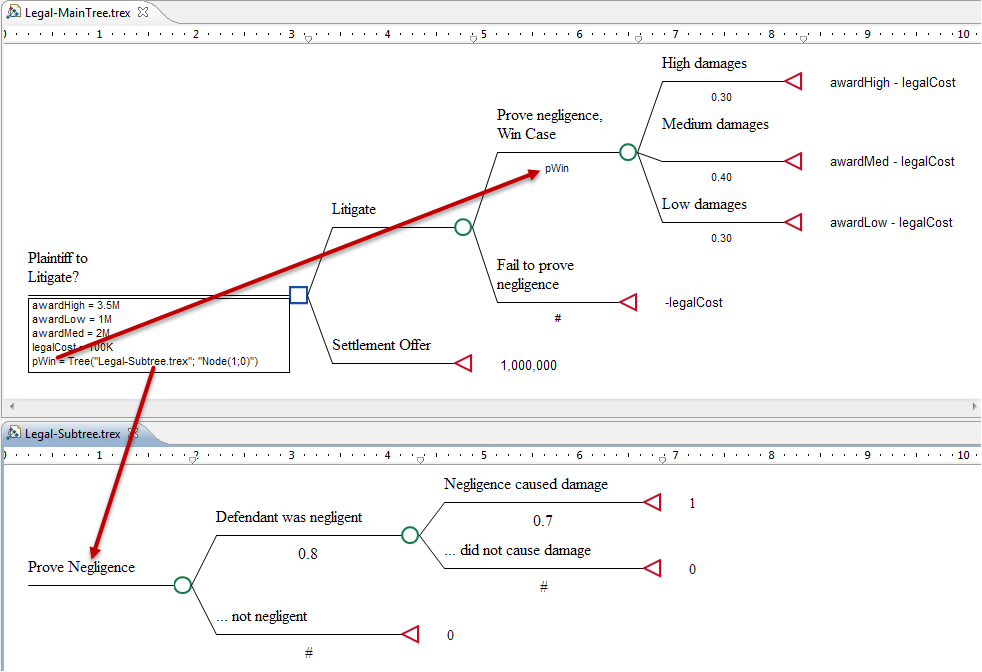
The subtree returns the 0.56 probability of proving negligence, which is then used for the variable pWin in the main tree.