57. Utility Functions and Risk Preferences
TreeAge Pro allows you to set up a risk preference utility function in a tree, which can be used to account for a decision maker’s aversion to risk.
57.0.1 Risk Preference: An illustration
Most decision makers are risk-averse to some degree. They are willing to pay a premium, small or large, to avoid risk. The decision maker’s risk preference can be incorporated into a decision tree.
Assume that a rich uncle offers you an opportunity to win some money. He proposes to flip a coin giving you the opportunity to receive either $10,000 or $1,000, depending on whether you correctly predict the outcome. If you call the flip correctly, you will receive $10,000, and if you are wrong you will receive $1,000.
To make this game more interesting, assume that your uncle complicates matters by offering an alternative opportunity. The alternative is also a coin flip. Under this one, you will receive $50,000 if you are correct, but you will have to pay him $5,000 in the event you lose on the coin flip. There will be only a single coin flip; it is up to you to choose between the two. As you will see, it may not be wise to base your decision solely on traditional expected value calculations.
The tree in Business tutorial examples, Risk Illustration, models your uncle’s offer.
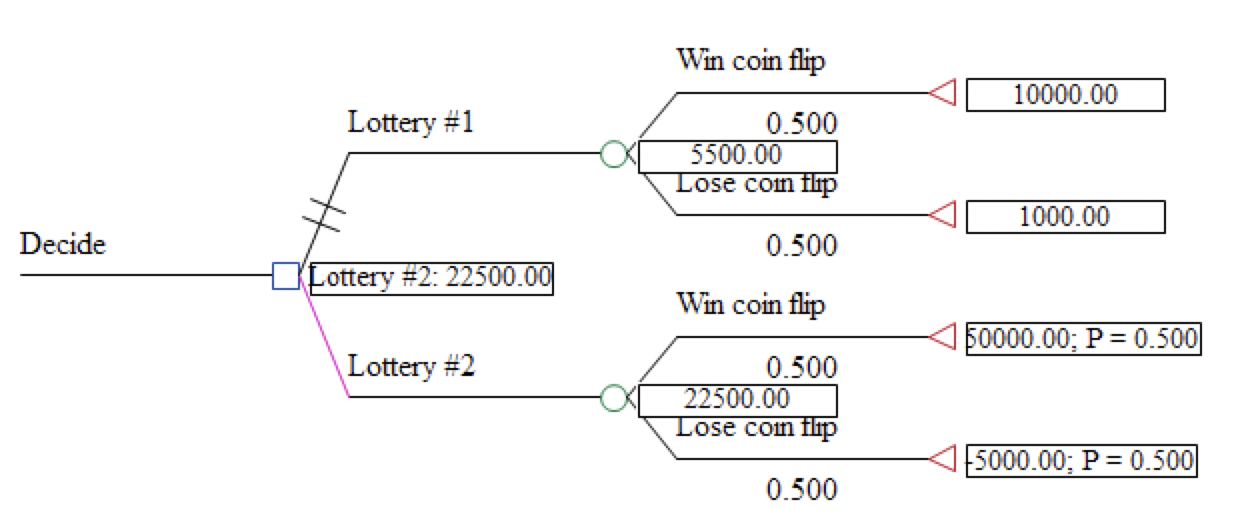
As the tree illustrates, there are two lotteries. Both provide the same (50 - 50) odds of winning, but they have different outcomes. You must choose one of them. On the basis of expected value, you should choose lottery #2. Its expected value ($22,500) is more than four times that of lottery # 1 ($5,500).
However, what about the risk posed in lottery #2 that you could actually end up losing $5,000? At least in lottery #1 there is no risk of being out-of pocket – you are guaranteed to win something. How one responds to the downside risk posed by lottery #2 involves a subjective analysis of the decision maker’s aversion to risk.
57.0.2 Certainty equivalents and risk aversion
Consider lottery #1 described above. The expected value is $5,500. Would you sell the opportunity to play this lottery for $4,000? If you were offered $3,000 by a third party who wanted to buy into the lottery, would you sell?
The minimum value for which you would sell the lottery is your certainty equivalent for this lottery. The certainty equivalent of a lottery can be perceived as the expected value of that lottery, adjusted for risk preference (the risk-adjusted expected value).
A certainty equivalent is similar to an expected value, in that it is a single numeric quantity which represents the value of an uncertain event. The certainty equivalent is a subjective measure; it is the answer to the question, “What is the minimum (or maximum) value for which I would trade this uncertainty?”
Now consider a situation which is undesirable from the start. Lottery #3 is a coin flip in which you will either owe your uncle $2,000 or you will owe him $12,000. In this situation, we are interested in finding the maximum amount that you are willing to pay to a third party to assume your obligation under the lottery. Would you pay $4,000? Or $5,000? Your answer to this question is your certainty equivalent for that lottery.
The certainty equivalent for a lottery is usually in the same numeric range as the expected value. The gap between the certainty equivalent and the expected value is a measure of risk aversion.
Most decision makers are risk-averse to some degree. They are willing to pay a premium, small or large, to avoid risk. Their certainty equivalent for any lottery will be lower than the lottery’s expected value. In contrast, a risk-seeking decision maker is one whose certainty equivalent for a lottery is higher than the lottery’s expected value. The risk taker is willing to pay a premium in order to participate in the lottery.
