Defining the problem

5.1 Defining the problem

Let us consider a Healthcare problem where we are comparing two strategies: a new treatment and the existing treatment. The new treatment is more costly but is more likely to be successful in treating the disease, leading to better health outcomes. We will build a model to choose the most cost-effective treatment.

The existing treatment of Radiation may eradicate or fail to eradicate the tumor. The new treatment of Surgery has the same two outcomes plus the additional outcome of death, as in the figure below. Treatment success will result in a longer life expectancy. However, we don’t yet know whether this increased life expectancy can justify the higher cost.

We can represent this problem with a decision tree based on the information above. However, we will also need numeric values associated with this problem, specifically: probabilities, treatment costs and life expectancy estimates. This will be the decision tree structure we build.

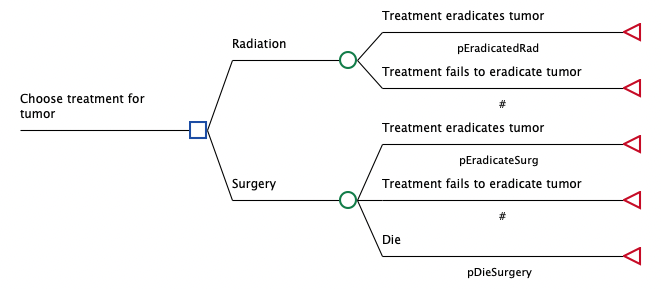
Healthcare Decision Tree

To evaluate the model, we need to set up the model to be analyzed using Cost-Effectiveness Analysis (CEA). The model also needs all the numeric values for model inputs such as cost, effectiveness and probabilities entering.

The numeric model inputs are as follows:

The new treatment (Surgery) will increase the probability of eradicating the tumor from 60% to 80%.
A person’s life expectancy is 10 years if the tumor is eradicated, but only 3 years if not.
With surgery, there is a 5% probability of death.
The costs associated with radiation and surgery are $30K and $50K respectively
The follow-up costs post-treatment are $2K per year until the end of life.

With this information, we can now build a decision tree which we will explain in the following sections.

Further topics:

Many cost-effectiveness models project into the future using Markov models. Markov models are covered in detail in the Chapter Building Markov Models. In this simple example, we will use estimated future cost and life expectancy instead building a model with time cycles (a Markov process).