Time dependence and using keywords

34.8 Time dependence and using keywords

Time dependence in Markov models uses the _stage counter. We often see the _stage counter being useful in defining the Markov termination condition. This section will describe other important functions of the _stage counter and other keywords.

34.8.1 Time dependence

Cycle zero (_stage = 0)

In TreeAge Pro Markov models, the first cycle is referred to as cycle 0 and the _stage counter is equal to 0 during this first cycle. For example, if a model’s cycle length is one year, cycle 0 represents the first year of the process; if this process started with an individual’s birth, cycle 0 would correspond to age 0 – i.e., the year prior to an individual’s first birthday.

The following events occur during the first cycle of a Markov process, while the keyword _stage is equal to 0:

The cohort is distributed among the Markov states according to the initial probabilities entered under the branches (the only time these probabilities are used);
Initial rewards are accumulated based on state membership;
The members of a state traverse the transition subtree based on the transition probabilities, and the percentage of the cohort at a transition node are assigned the transition rewards in the path back to the state (before entering new states for the next cycle).

You should ensure that references to tables in initial and transition probability expressions, as well as in initial state rewards and transition rewards, will work correctly when _stage = 0.

The incremental state reward expressions are not accumulated during cycle 0; only the initial rewards are evaluated. The initial probabilities determine which states are populated in cycle 0 and where initial state rewards are required. If half-cycle correction is not used, the initial state reward for a state is often the same as the incremental reward; see the section on Half-Cycle correction for more details.

Using tables of time-dependent transition probabilities – an example with Background Mortality

The Three-State Markov model in the example files is an example of a Markov chain — a Markov model in which all probabilities and other parameters remain constant over time. In the kinds of Markov models used to represent healthcare issues, probabilities and other values often vary over time. This kind of model is referred to sometimes as a Markov process.

In the TreeAge Pro Healthcare module, any expression in a Markov model (not just the termination condition) can reference tables of stage-dependent values using the _stage counter. Other kinds of time-dependent expressions can also be created using the _tunnel counter, trackers (in microsimulation models), etc.

This example tutorial requires two things:

A copy of the Three-State Markov model from the Health Care tutorial examples: Three-State Markov.trex.
A table in the model (which you can add below) called tMort to hold time-varying probabilities. Follow the instructions below to create the table. If you have additional questions about working with tables, refer to the section Creating, Editing and Referencing Tables.

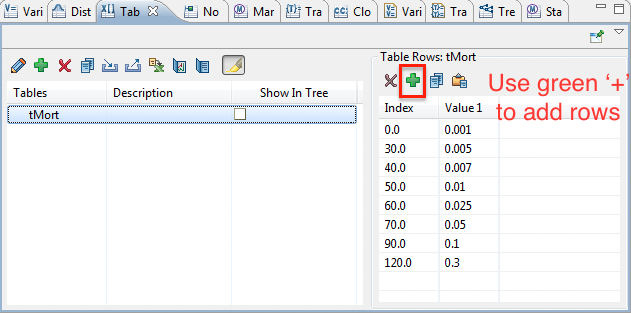
To create a new table for use in a tree:

Choose Views > Tables from the toolbar to open to Tables View.
Click the "add" toolbar button. This will open the Add/Change Table Dialog.
Enter the table name tMort and select the "Use linear interpolation" option for missing rows.
Click OK to save the table and close the dialog.
In the Tables View, select the table and then click the "add" button in the "Table Rows" section of the Tables View on the right-hand side. Click seven more times to add a total of eight rows.
Edit the data in each row to match the data presented below.

Now we can update the Three-State Markov model to use the new table of mortality probabilities.

Note: If you have a table in Excel you can just copy the headers and data and then paste the information into the table. This saves entering each row of data.

To look up a transition probability in a table:

First define the variable startAge at the root node and define it with the value 30. This section may help: Creating Variables.
Select the die branch of the Disease state, and change its probability to the formula tMort[startAge+_stage].

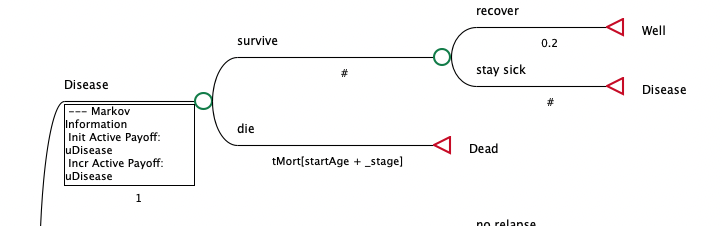
This adjusted model is also in the tutorials as Three-State Markov-Time.trex, which you can open to see the model with the table incorporated.

In this revised model, in place of a fixed probability of death from other causes, TreeAge Pro will calculate the transition probability at every cycle using the table lookup tMort[startAge+_stage]. The first set of transitions in the Markov process, when _stage = 0, will use the value returned from tMort[30+0], which is evaluated as 0.005.

Each subsequent cycle will use a higher mortality probability, because the values in the tMort table increase as the indexes increase. Also relevant in this case, when you reference a missing index, the table is currently set to interpolate between existing indexes. In the example, the missing value for cycle 1 when the table reference is tMort[31] will be calculated using linear interpolation between the table values for indexes 30 and 40. The interpolated probability will be 0.0052. Missing rows at subsequent cycles will be similarly calculated.

If you now roll back the tree, the Markov node should display an expected value of 34.818 – significantly higher than the roll back value calculated in the previous chapter because the early probabilities of death in the table are lower than the original 0.01 probability of mortality. The updated tree is available with the name Three-State Markov-Time.trex for your review.

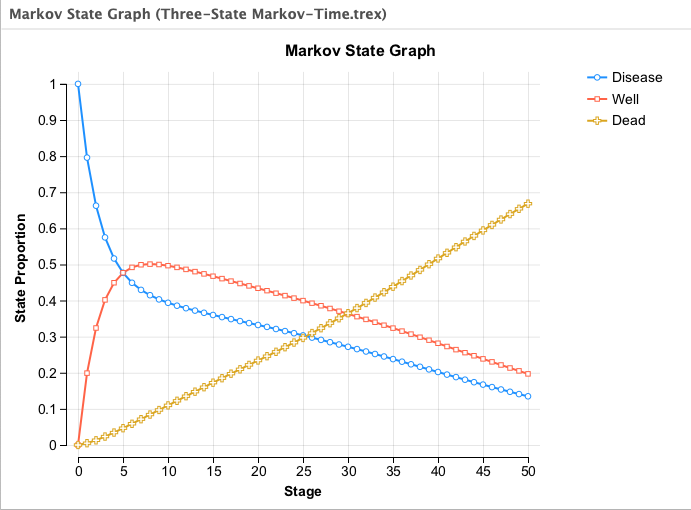
If you run a Markov cohort analysis in the new version of the tree, and compare the new state probabilities graph with the graph generated in the previous chapter, you will see that the cohort transitions to death considerably more slowly.

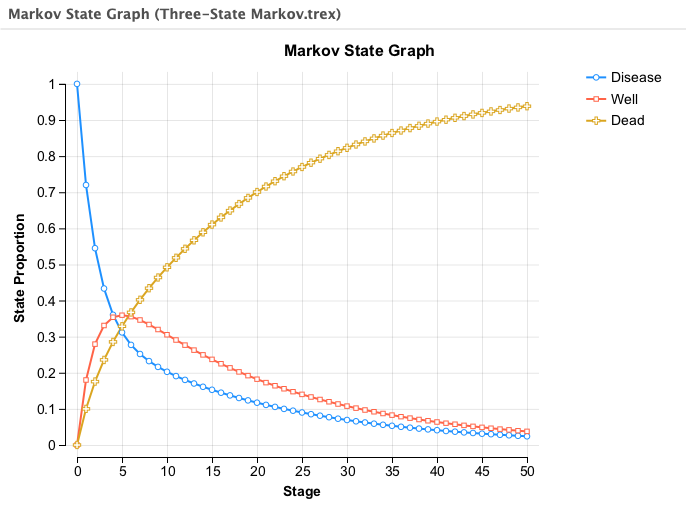
Below is the State Probabilities Graph from the original model with a fixed probability of death.

Note the difference in the new model with the probability of death increasing over time.

34.8.2 Markov Keywords

TreeAge Pro provides several Markov keywords — built-in variables which are available only in a Markov node or its subtree. The first two listed in the table below are integer counters.

Keywords	Definition
_stage	The number of cycles that have passed (starts at 0 for first cycle).
_tunnel	The number of cycles spent continuously in a tunnel state.
_stage_reward	The reward accumulated in the previous cycle for the active payoff
_stage_cost, _stage_eff	the reward accumulated in the previous cycle for the active cost and effectiveness payoffs
_stage_att1, _stage_att2, etc	the reward accumulated in the previous cycle for that payoff number (1, 2, etc.)
_total_reward	the cumulative reward of all previous cycles for the active payoff
_total_cost, _total_eff	the cumulative reward of all previous cycles for the active cost and effectiveness payoffs
_total_att1, _total_att2, etc	the cumulative reward of all previous cycles for the specified payoff number (1, 2, etc.)
StateProb( )	This is a special function for accessing current state probabilities during analysis

Run a Cohort Analysis on Health Care Example model tree Markov Keywords.trex to see a few of the above keywords written to the calculation trace console. Compare the cohort analysis results to the console and you can see what those keywords do.

The _stage counter is useful in defining the Markov termination condition. This section will describe other important functions of the _stage counter and other keywords.