34.5 Half-Cycle Correction (HCC)
Real processes occur in continuous time, with transitions and other events occurring throughout an interval of time. However, a Markov process occurs as a discrete sequence of snapshots, which can lead to over counting Markov rewards.
Traditional Markov models accumulate the full cycle's state reward at the beginning of each cycles with transitions understood to occur at the end of each cycle, even though some portion of the cohort will leave the state during the cycle. Expected values will therefore overestimate life expectancy by about half of a cycle (1/2 year in a one-year cycle length model).
Consider the simple example of life expectancy in a simple model with health states Alive and Dead. In each cycle, some portion of the cohort is alive and accumulates 1 life year. In reality, however, deaths will occur on average halfway through a cycle. So, someone who dies during a cycle should lose half of the reward they received at the beginning of the cycle (e.g., -0.5 years of life expectancy in a one-year cycle length model).
There are two ways in TreeAge to adjust for this over accumulation:
-
Half-Cycle Correction (HCC) - this section.
What does HCC look like?
Half-cycle correction subtracts "half a reward" assigned in the first cycle of the process (that is at _stage 0) — i.e., by setting a state’s initial reward (Init Rwd) to one-half of its incremental reward (Incr Rwd). The portion of the cohort that remains in the health state at the end of the process is then given back the "half a reward" after the last cycle in the final reward (Final Rwd) for all non-dead states. This is part of why state rewards are separated into three parts: Init, Incr and Final.
Some modelers choose to apply half-cycle correction as a toll at each transition out of a non-dead state, but this is more complicated and prone to error.
To perform half-cycle correction:
-
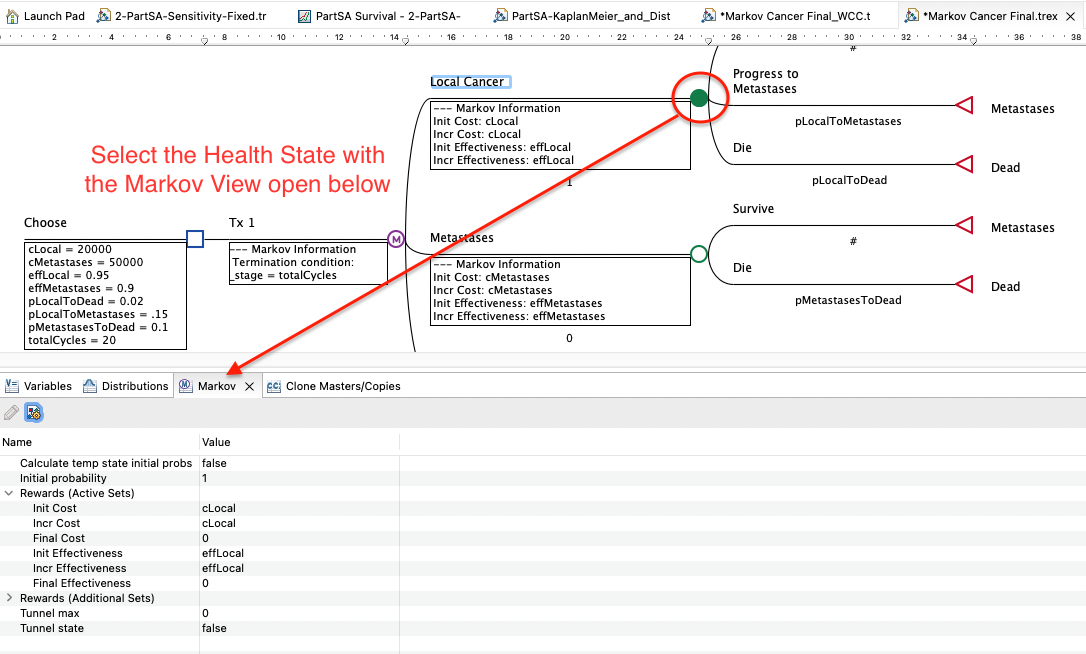
Select a Markov state node (in the image below this is Local Cancer).
-
Open the Markov View.
-
Enter the initial and incremental rewards. In the images, we have cLocal for both Init and Incr Costs.
-
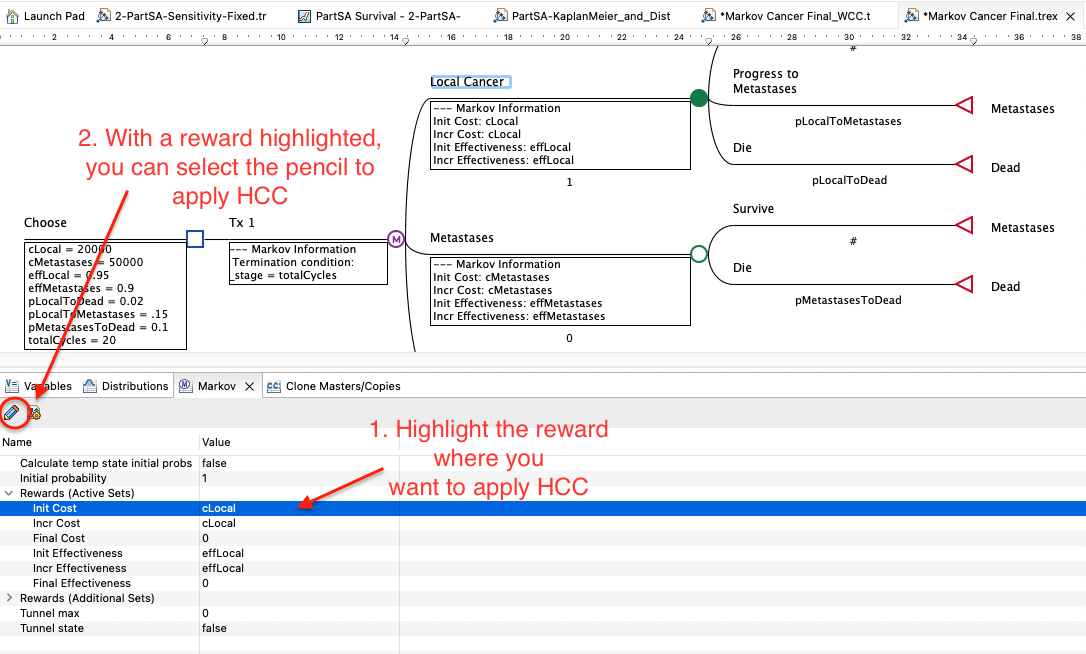
In the Markov View, select/highlight a reward to HCC for the appropriate payoff set. In this case we will choose the Cost.
-
Click on the "pencil" icon in the view's toolbar to open the State Reward Dialog.
-
Click the Half-Cycle Correct button in the State Reward Dialog.
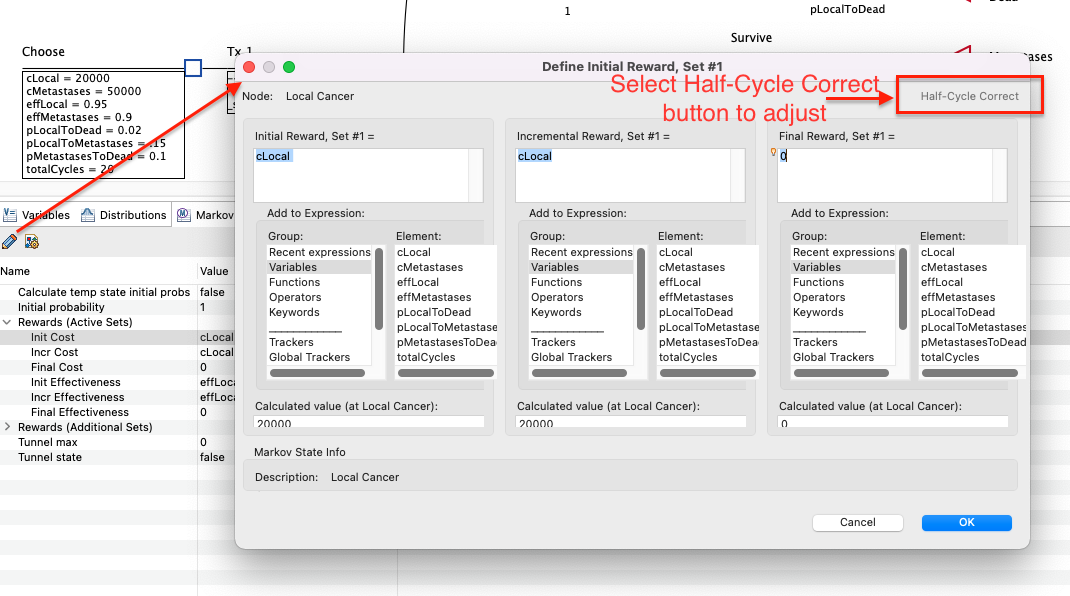
The initial and final rewards will be updated as below.
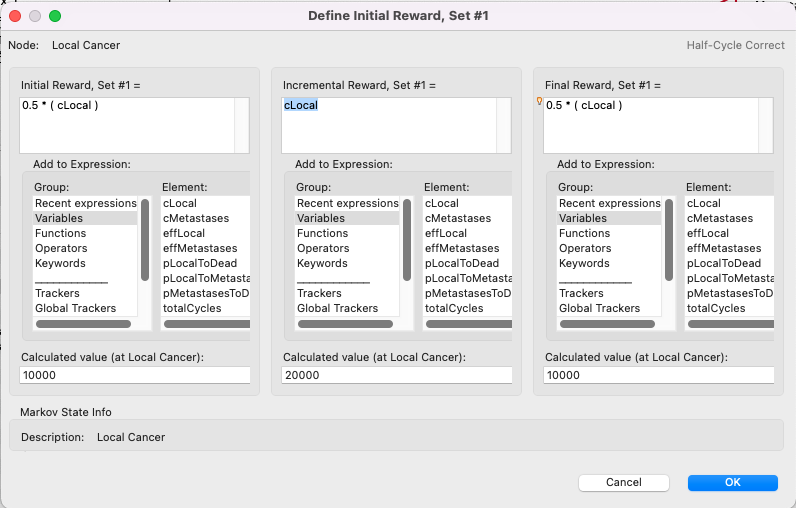
Any reward that is a function of life expectancy (i.e., medication costs that occur gradually over a cycle) should be corrected in the same way.
NOTE: Be careful when applying HCC using the steps above. Clicking the Half-cycle Correction button will delete any entries in the Initial and Final rewards and replace them with half the Incremental Reward. If you have any additional entries in those fields (particularly up-front costs in the initial reward), be sure to add those back into the model after applying HCC.
Reporting with Half-Cycle Correction, Within-Cycle Correction or neither is covered in the section Markov Cohort Analysis Output.
