35.6 Sampling probabilities from a multivariate Dirichlet distribution
If a chance node has more than two branches with non-negligible probabilities, performing a sensitivity analysis or Monte Carlo simulation that changes the values of these probabilities can be problematic. One option is to normalize the chance node’s probability expressions. For example, if a node has three outcomes, A, B, and C, rather than assigning variables to two probabilities and using the # remainder for the third, you could do the following: assign three expressions that always sum to 1.0, such as pA/(pA+pB+pC) and pB/(pA+pB+pC) and pC/(pA+pB+pC). No matter what values (>= 0) are assigned to pA, pB, and pC, the three normalized probabilities will always sum to 1.0. (The # remainder could still be used in place of one of these.)
TreeAge Pro offers a similar solution using a special, multivariate form of the beta probability distribution, called a Dirichlet distribution. This distribution can be used to represent the uncertainty in all of the probabilities of a chance event. During Monte Carlo simulation, the distribution can sample probabilities for each branch using normalization to ensure that the probabilities always sum to 1.0.
If the distribution is parameterized with a list of three positive alpha values, as shown here, TreeAge Pro will samples three independent Gamma[alpha, beta=1.0] distributions and normalize these to create a list of three probabilities.
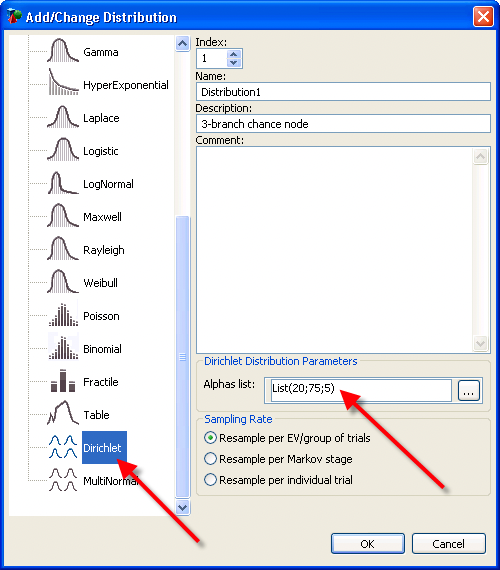
For documentation on creating and editing distributions, refer to the section Distributions: creating, editing and using.
The Dist() function is used with a second argument to indicate which branch (i.e., alpha) to use. The Health Care tutorial example model, "Dirichlet Simple", is shown below.
Rolling back the tree shows the mean values of the probabilities, which are simply the normalized alpha parameters.
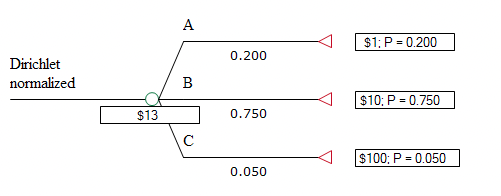
Performing a simulation in the example tree shows the effect of sampling independent Gamma distribution values based on the list of alpha parameters, and then normalizing. For each iteration of the simulation, a different set of Gamma random variates is drawn. Each iteration results in a different sum, as well as different ratios of the Gamma random variates to the sum (i.e., the probabilities), but normalization ensures that the resulting probabilities sum to 1.0.
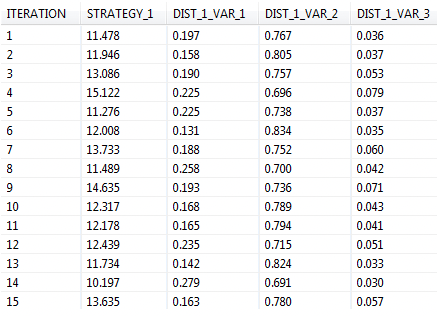
The following output from a PSA simulation shows the different probability values generated by the Dirichlet distribution for each simulation iteration. Note that the probability values are centered around the respective mean values.