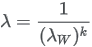13.5 Distribution formulas
This section provides the formulas TreeAge Pro uses to generate distributions.
Hint: To find distributions quickly, use the search option in your browser and enter the distribution name.
13.5.1 Normal distribution
| Formula |
|
| Domain |
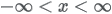
|
| Parameters |
Mean: Standard deviation: |
13.5.2 Uniform distribution continuous – (real numbers)
| Formula |
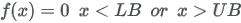
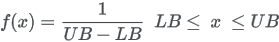
|
| Domain |
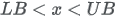
|
| Parameters |
LB lower bound |
13.5.3 Uniform distribution discrete (integer numbers)
| Formula |
|
| Domain |
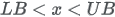
|
| Parameters |
LB and UB integers. LB lower bound |
13.5.4 Triangular distribution
| Formula |
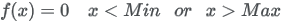

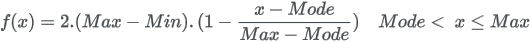
|
| Domain | Min ≤ x ≤ Max |
| Parameters | Min, Mode (likeliest), Max |
13.5.5 Fractile distributions (10/50/90 et al)
| Formula |
|
| Domain | LV, MV, HV |
| Parameters | LV, MV, HV |
13.5.6 Beta distribution discrete (integer numbers)
| Formula |
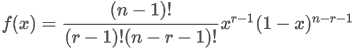
|
| Domain |
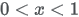
|
| Parameters |
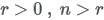
|
| Details |

|
13.5.7 Beta distribution continuous (real numbers)
| Formula |
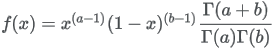
|
| Domain |
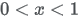
|
| Parameters |
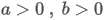
|
| Details |

Parameters a and b can be parameterized from a mean μ and standard deviation σ: 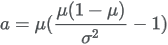 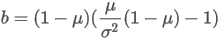 |
More continuous distributions
13.5.8 Dirichlet distribution (multivariate, normalized beta)
| Formula |

where 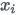 are sampled from Gamma distributions: are sampled from Gamma distributions: The parameters 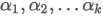 are specified in the Alphas list of the Dirichlet Distribution dialog using are specified in the Alphas list of the Dirichlet Distribution dialog using |
| Domain |
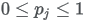 where where 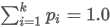 |
| Parameters |
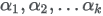
|
| Details | See section Sampling probabilities from a multivariate Dirichlet distribution . |
13.5.9 Chi distribution
| Formula |
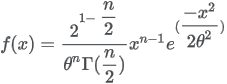
|
| Domain |

|
| Parameters |

|
13.5.10 Chi-Squared distribution
| Formula |
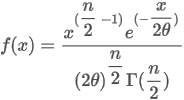
|
| Domain |

|
| Parameters |

|
13.5.11 Erlang distribution
| Formula |
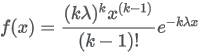
|
| Domain |

|
| Parameters | 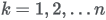 integer, integer,  |
Please note that the Erlang probability density function can also be represented using a related formula (as shown on Wikipedia):
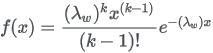
To convert the above scale parameter 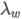 to TreeAge Pro’s scale parameter please use the following formula:
to TreeAge Pro’s scale parameter please use the following formula:
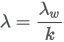
13.5.12 Exponential distribution
| Formula |

|
| Domain |

|
| Parameters |

|
Survival Function information:
TreeAge Pro survival function form:

Corresponding parameters from other software packages (STATA and SAS):

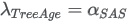
R SURVREG function output. (Note: negative sign before intercept!)

R FLEXSURVREG function output.
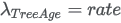
13.5.13 Gamma distribution
| Formula |
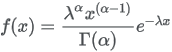
|
| Domain |

|
| Parameters |
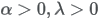
|
| Details |
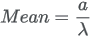
The parameters a and
|
13.5.14 Generalized Gamma distribution
| Formula |
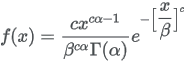
|
| Domain |

|
| Parameters |

|
Survival Function information:
TreeAge Pro survival function form:
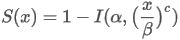 where
where
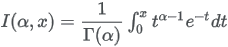
Corresponding parameters from other software packages:
-
STATA implementation of GenGamma is not compatible
-
SAS does not support GenGamma
-
R SURVREG does not support GenGamma
-
R FLEXSURVREG function supports GenGamma.orig and GenGamma.
GenGamma Original has more straightforward correspondence to TreeAge Pro

GenGamma has a more complex parameterization. For positive Q parameter use the following formulas:
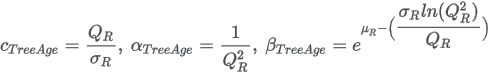
13.5.15 Gompertz distribution
| Formula |
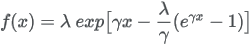
|
| Domain |

|
| Parameters |
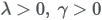
|
|
Alternative |
|
|
TreeAge Pro also implements |

|
| Parameters | where 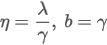 |
Survival Function information:
TreeAge Pro survival function form:
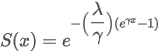
Corresponding parameters from other software packages:
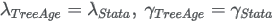
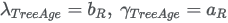
13.5.16 Hyper-exponential distribution
| Formula |
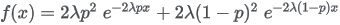
|
| Domain |

|
| Parameters |
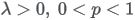
|
13.5.17 Laplace distribution
| Formula |
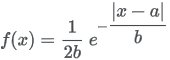
|
| Domain |
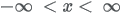
|
| Parameters |

|
13.5.18 Logistic distribution
| Formula |
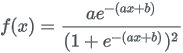
|
| Domain |
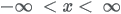
|
| Parameters |
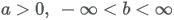
|
13.5.19 Log-Logistic distribution
| Formula |
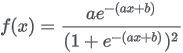
|
| Domain |
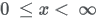
|
| Parameters |
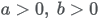
|
Survival Function information:
TreeAge Pro survival function form:
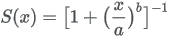
Corresponding parameters from other software packages (Stata and SAS):
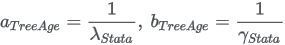
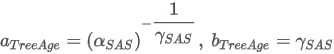
R SURVREG function output:

R FLEXSURVREG function output:
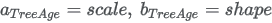
13.5.20 Lognormal distribution
| Formula |
|
| Domain |

|
| Parameters |
|
| Parameters |
The parameters μ and σ are the mean and standard deviation respectively, from the distribution of the ln(x), and can be approximated:
|
Survival Function information:
TreeAge Pro survival function form:
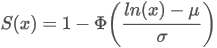
where  is the cumulative distribution function of the standard normal distribution (i.e., N(0,1)).
is the cumulative distribution function of the standard normal distribution (i.e., N(0,1)).
Corresponding parameters from other software packages:
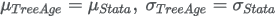
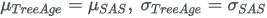
R SURVREG function output:
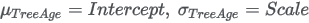
R FLEXSURVREG function output:

R FLEXSURVREG (newer version 2023?) function output:

The R statistical packages keep refining the parameterizations of distributions, please examine the associated documentation for their survival functions to determine which parameterization is appropriate for your model.
13.5.21 Maxwell distribution
| Formula |
|
| Domain |
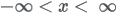
|
| Parameters |
|
13.5.22 PERT distribution continuous
| Formula |
This is the same formula as Beta continuous distribution, but with z rescaled by the PERT parameters. |
| Domain |
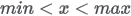
|
| Parameters |
Min, Mode (Likeliest), Max, Shape |
| Details |
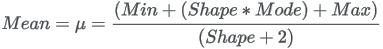
The underlying Beta parameters a and b are functions of the PERT parameters:
|
| Pert Sigma |
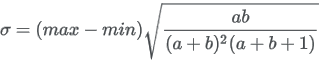
|
13.5.23 Rayleigh distribution
| Formula |
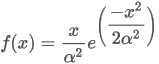
|
| Domain |

|
| Parameters |

|
13.5.24 Weibull distribution
| Formula |
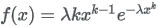
|
| Domain |

|
| Parameters |
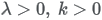
|
| Alternative representation of PDF |
Please note that the Weibull probability density function can also be represented using a related formula (as shown on Wikipedia):
To convert the above scale parameter
The shape parameter k is identical in both formulas. |
| Note | For values of k smaller than 0.05 the resulting samples are likely to fall outside of numerical precision of x<~5.0∙10^(-324) or x>~1.8∙10^308, these values will result in calculation errors, where expressions could not be evaluated. |
Survival Function information:
TreeAge Pro survival function form:

Corresponding parameters from other software packages (Stata, SAS):
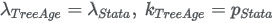
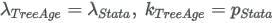
R SURVREG function output (Use TreeAge Pro alternate parameterization).

R FLEXSURVREG function output (Use TreeAge Pro alternate parameterization)

More discrete distributions
13.5.25 Binomial distribution
| Formula |
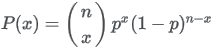
|
| Domain |
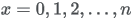
|
| Parameters |

|
13.5.26 Poisson distribution
| Formula |
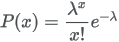
|
| Domain |
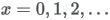
|
| Parameters |

|
Other distributions
13.5.27 TableProb distribution
The TableProb distribution takes as its input either a probability table or cumulative probability table. Typical use case of this distribution is to sample time to death directly from a mortality table.
The first entry in the probability table and cumulative probability table has to be equal to 0 and the last entry has to be equal to 1. The index for these tables represents time in cycles (typically year). Make sure that your model time horizon is shorter than the last time entry in the table. For model time horizon of 80 years make sure that the probability table or the cumulative probability table has entries beyond 80 years, at least there is an entry 1 at index 81.
Sampling from cumulative probability table is straightforward. A random number between 0 and 1 is sampled. The random number is than used for reverse look- up of the indices (cycle time) that contain the random number. Finally linear
interpolation is performed to return the fraction cycle time corresponding to the random number.
Sampling from probability table involves an internal step of converting the probability table to cumulative probability table. The following calculations are performed to convert probability table to cumulative probability table:
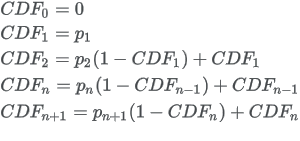
Additional option for conversion of probability tables to cumulative probability tables is interpolation. If the probability table has definitions for each integer value from 0, 1, ..., N-1, N you do not need to use interpolation. However, if the probability table is “sparse” e.g. 0, 5, 10, 15, ..., N then interpolation option will enable creation of cumulative probability table that will approximate results obtained from a Markov model using the “sparse” probability table.
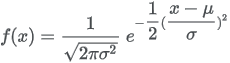
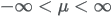

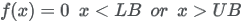 or x is not an integer.
or x is not an integer. 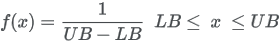
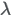 can be parameterized from a mean
can be parameterized from a mean 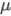 and standard deviation
and standard deviation 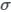 :
: 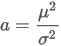
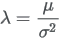
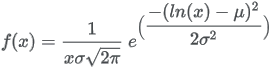
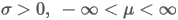


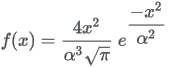

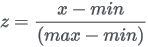 for
for 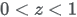
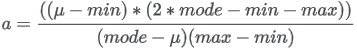
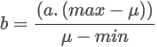

 to TreeAge Pro’s scale parameter
to TreeAge Pro’s scale parameter 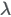 please use the following formula:
please use the following formula: